
The area A is equal to the square root of the semiperimeter s times semiperimeter s minus side a times semiperimeter s minus a times semiperimeter s minus base b. Determine the lengths of the sides AB, AC triangle A Right angled We built a square with the same area as the right triangle with legs 12 cm. KLM is an isosceles triangle with a right angle at point K. Points L and M split the AC side into three equal lines. You can find the area of an isosceles triangle using the formula: In a triangle ABC with the side BC of length 2 cm. The semiperimeter s is equal to half the perimeter. Given the perimeter, you can find the semiperimeter.
Triangle isosceles plus#
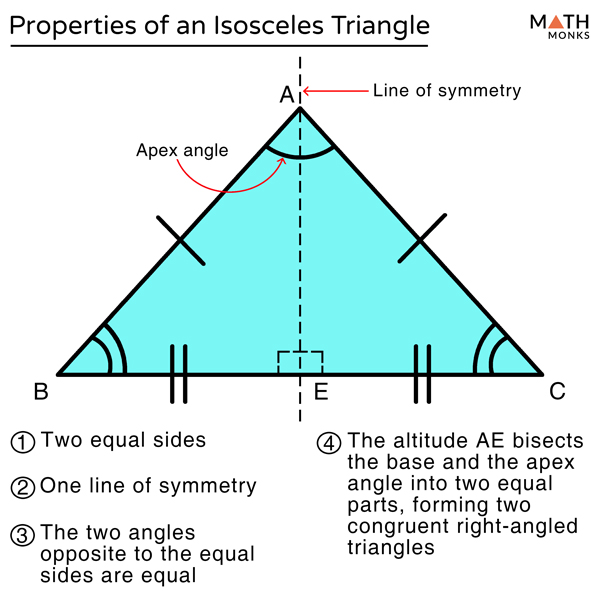
Thus, the perimeter p is equal to 2 times side a plus base b. You can find the perimeter of an isosceles triangle using the following formula: Given the side lengths of an isosceles triangle, it is possible to solve the perimeter and area using a few simple formulas. The vertex angle β is equal to 180° minus 2 times the base angle α. Use the following formula to solve the vertex angle: The base angle α is equal to quantity 180° minus vertex angle β, divided by 2. Use the following formula to solve either of the base angles: Given any angle in an isosceles triangle, it is possible to solve the other angles.
Triangle isosceles how to#
How to Calculate the Angles of an Isosceles Triangle The side length a is equal to the square root of the quantity height h squared plus one-half of base b squared. Use the following formula also derived from the Pythagorean theorem to solve the length of side a: The base length b is equal to 2 times the square root of quantity leg a squared minus the height h squared. Use the following formula derived from the Pythagorean theorem to solve the length of the base side: Given the height, or altitude, of an isosceles triangle and the length of one of the sides or the base, it’s possible to calculate the length of the other sides. How to Calculate Edge Lengths of an Isosceles Triangle We have a special right triangle calculator to calculate this type of triangle. Note, this means that any reference made to side length a applies to either of the identical side lengths as they are equal, and any reference made to base angle α applies to either of the base angles as they are also identical. When references are made to the angles of a triangle, they are most commonly referring to the interior angles.īecause the side lengths opposite the base angles are of equal length, the base angles are also identical. The two interior angles adjacent to the base are called the base angles, while the interior angle opposite the base is called the vertex angle. The equilateral triangle, for example, is considered a special case of the isosceles triangle. However, sometimes they are referred to as having at least two sides of equal length.
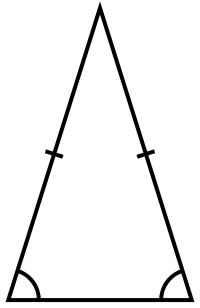
Isosceles triangles are typically considered to have exactly two sides of equal length. The third side is often referred to as the base. The two angles opposite the legs are equal and are always acute, so the classification of the triangle as acute, right, or obtuse depends only on the angle between its two legs.An isosceles triangle is a triangle that has two sides of equal length. Every isosceles triangle has an axis of symmetry along the perpendicular bisector of its base. The other dimensions of the triangle, such as its height, area, and perimeter, can be calculated by simple formulas from the lengths of the legs and base. The two equal sides are called the legs and the third side is called the base of the triangle. Isosceles triangles have been used as decoration from even earlier times, and appear frequently in architecture and design, for instance in the pediments and gables of buildings. The mathematical study of isosceles triangles dates back to ancient Egyptian mathematics and Babylonian mathematics. Examples of isosceles triangles include the isosceles right triangle, the golden triangle, and the faces of bipyramids and certain Catalan solids. Sometimes it is specified as having two and only two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. In geometry, an isosceles triangle is a triangle that has two sides of equal length.


 0 kommentar(er)
0 kommentar(er)
